a) Saat batu berada di titik tertinggi, kecepatan batu adalah nol dan percepatan yang digunakan adalah percepatan gravitasi. Dengan rumus GLBB:

b) Waktu yang diperlukan batu untuk mencapai titik tertinggi:

c) Lama batu berada di udara adalah dua kali lama waktu yang diperlukan untuk mencapai titik tertinggi.
t = (2)(5) = 10 sekon
Soal No. 2Sebuah mobil bergerak dengan kelajuan awal 72 km/jam kemudian direm hingga berhenti pada jarak 8 meter dari tempat mulainya pengereman. Tentukan nilai perlambatan yang diberikan pada mobil tersebut!
PembahasanUbah dulu satuan km/jam menjadi m/s kemudian gunakan persamaan untuk GLBB diperlambat:

Soal No. 3Perhatikan grafik berikut ini.

Dari grafik diatas tentukanlah:
a. jarak tempuh gerak benda dari t = 5 s hingga t = 10 s
b. perpindahan benda dari t = 5 s hingga t = 10 s
PembahasanJika diberikan graik V (kecepatan) terhadap t (waktu) maka untuk mencari jarak tempuh atau perpindahan cukup dari luas kurva grafik V-t. Dengan catatan untuk jarak, semua luas bernilai positif, sedang untuk menghitung perpindahan, luas diatas sumbu t bernilai positif, di bawah bernilai negatif.
 Soal No. 4
Soal No. 4Seekor semut bergerak dari titik A menuju titik B pada seperti terlihat pada gambar berikut.

Jika r = 2 m, dan lama perjalanan semut adalah 10 sekon tentukan:
a) Kecepatan rata-rata gerak semut
b) Kelajuan rata-rata gerak semut
PembahasanTerlebih dahulu tentukan nilai perpindahan dan jarak si semut :
Jarak yang ditempuh semut adalah dari A melalui permukaan lengkung hingga titik B, tidak lain adalah seperempat keliling lingkaran.
Jarak =
1/
4 (2πr) =
1/
4 (2π x 2) = π meter
Perpindahan semut dilihat dari posisi awal dan akhirnya , sehingga perpindahan adalah dari A tarik garis lurus ke B. Cari dengan phytagoras.
Perpindahan = √ ( 2
2 + 2
2 ) = 2√2 meter.
a) Kecepatan rata-rata = perpindahan : selang waktu
Kecepatan rata-rata = 2√2 meter : 10 sekon = 0,2√2 m/s
b) Kelajuan rata-rata = jarak tempuh : selang waktu
Kelajuan rata- rata = π meter : 10 sekon = 0,1 π m/s
Soal No. 5Pesawat Burung Dara Airlines berangkat dari kota P menuju arah timur selama 30 menit dengan kecepatan konstan 200 km/jam. Dari kota Q berlanjut ke kota R yang terletak 53
o terhadap arah timur ditempuh selama 1 jam dengan kecepatan konstan 100 km/jam.

Tentukan:
a) Kecepatan rata-rata gerak pesawat
b) Kelajuan rata-rata gerak pesawat
PembahasanSalah satu cara :
Terlebih dahulu cari panjang PQ, QR, QR', RR', PR' dan PR

PQ = V
PQ x t
PQ = (200 km/jam) x (0,5) jam = 100 km
QR = V
QR x t
QR = (100 km/jam) x (1 jam) = 100 km
QR' = QR cos 53
o = (100 km) x (0,6) = 60 km
RR' = QR sin 53
o = (100 km) x (0,8) = 80 km
PR' = PQ + QR' = 100 + 60 = 160 km
PR = √[ (PR' )
2 + (RR')
2 ]
PR = √[ (160 )
2 + (80)
2 ] = √(32000) = 80√5 km
Jarak tempuh pesawat = PQ + QR = 100 + 100 = 200 km
Perpindahan pesawat = PR = 80√5 km
Selang waktu = 1 jam + 0,5 jam = 1,5 jam
a) Kecepatan rata-rata = perpindahan : selang waktu = 80√5 km : 1,5 jam = 53,3 √5 km/jam
b) Kelajuan rata-rata = jarak : selang waktu = 200 km : 1,5 jam = 133,3 km/jam
Soal No. 6Diberikan grafik kecepatan terhadap waktu seperti gambar berikut:

Tentukan besar percepatan dan jenis gerak dari:
a) A - B
b) B - C
c) C - D
PembahasanMencari percepatan (a) jika diberikan grafik V-t :
a = tan θ
dengan θ adalah sudut kemiringan garis grafik terhadap horizontal dan tan suatu sudut adalah sisi depan sudut dibagi sisi samping sudut. Ingat : tan-de-sa
a) A - B
a = (2 − 0) : (3− 0) =
2/
3 m/s
2(benda bergerak lurus berubah beraturan / GLBB dipercepat)
b) B - C
a = 0 (garis lurus, benda bergerak lurus beraturan / GLB)
c) C - D
a = (5 − 2) : (9 − 7) =
3/
2 m/s
2(benda bergerak lurus berubah beraturan / GLBB dipercepat)
Soal No. 7Dari gambar berikut :

Tentukan:
a) Jarak tempuh dari A - B
b) Jarak tempuh dari B - C
c) Jarak tempuh dari C - D
d) Jarak tempuh dari A - D
Pembahasana) Jarak tempuh dari A - B
Cara Pertama
Data :
V
o = 0 m/s
a = (2 − 0) : (3− 0) =
2/
3 m/s
2t = 3 sekon
S = V
o t +
1/
2 at
2S = 0 +
1/
2 (
2/
3 )(3)
2 = 3 meter
Cara Kedua
Dengan mencari luas yang terbentuk antara titik A, B dang angka 3 (Luas Segitiga = setengah alas x tinggi) akan didapatkan hasil yang sama yaitu 3 meter
b) Jarak tempuh dari B - C
Cara pertama dengan Rumus GLB
S = Vt
S = (2)(4) = 8 meter
Cara kedua dengan mencari luas yang terbentuk antara garis B-C, angka 7 dan angka 3 (luas persegi panjang)
c) Jarak tempuh dari C - D
Cara Pertama
Data :
V
o = 2 m/s
a =
3/
2 m/s
2t = 9 − 7 = 2 sekon
S = V
o t +
1/
2 at
2S = (2)(2) +
1/
2 (
3/
2 )(2)
2 = 4 + 3 = 7 meter
Cara kedua dengan mencari luas yang terbentuk antara garis C-D, angka 9 dan angka 7 (luas trapesium)
S = 1/2 (jumlah sisi sejajar) x tinggi
S = 1/2 (2+5)(9-7) = 7 meter.
d) Jarak tempuh dari A - D
Jarak tempuh A-D adalah jumlah dari jarak A-B, B-C dan C-D
Soal No. 8Mobil A dan B dalam kondisi diam terpisah sejauh 1200 m.

Kedua mobil kemudian bergerak bersamaan saling mendekati dengan kecepatan konstan masing-masing V
A = 40 m/s dan V
B = 60 m/s.
Tentukan:
a) Jarak mobil A dari tempat berangkat saat berpapasan dengan mobil B
b) Waktu yang diperlukan kedua mobil saling berpapasan
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
PembahasanWaktu tempuh mobil A sama dengan waktu tempuh mobil B, karena berangkatnya bersamaan. Jarak dari A saat bertemu misalkan X, sehingga jarak dari B (1200 − X)
t
A = t
BSA/
VA =
SB/
VB( x )/
40 =
( 1200 − x ) /
606x = 4( 1200 − x )
6x = 4800 − 4x
10x = 4800
x = 480 meter
b) Waktu yang diperlukan kedua mobil saling berpapasan
x = V
A t
480 = 40t
t = 12 sekon
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
S
B =V
B t = (60) (12) = 720 m
Soal No. 9Diberikan grafik kecepatan terhadap waktu dari gerak dua buah mobil, A dan B.

Tentukan pada jarak berapakah mobil A dan B bertemu lagi di jalan jika keduanya berangkat dari tempat yang sama!
PembahasanAnalisa grafik:
Jenis gerak A → GLB dengan kecepatan konstan 80 m/s
Jenis gerak B → GLBB dengan percepatan a = tan α = 80 : 20 = 4 m/s
2Kedua mobil bertemu berarti jarak tempuh keduanya sama, misal keduanya bertemu saat waktu t
S
A = S
BV
A t =V
oB t +
1/
2 at
280t = (0)t +
1/
2 (4)t
22t
2 − 80t = 0
t
2 − 40t = 0
t(t − 40) = 0
t = 0 sekon atau t = 40 sekon
Kedua mobil bertemu lagi saat t = 40 sekon pada jarak :
S
A = V
A t = (80)(40) = 3200 meter
Soal No. 10 (Gerak Vertikal ke Bawah / Jatuh Bebas)Sebuah benda jatuh dari ketinggian 100 m. Jika percepatan gravitasi bumi 10 m/s
2 tentukan:
a) kecepatan benda saat t = 2 sekon
b) jarak tempuh benda selama 2 sekon
c) ketinggian benda saat t = 2 sekon
d) kecepatan benda saat tiba di tanah
e) waktu yang diperlukan benda hingga tiba di tanah
Pembahasana) kecepatan benda saat t = 2 sekon
Data :
t = 2 s
a = g = 10 m/s
2V
o = 0 m/s
V
t = .....!
V
t = V
o + at
V
t = 0 + (10)(2) = 20 m/s
c) jarak tempuh benda selama 2 sekon
S = V
ot +
1/
2at
2S = (0)(t) +
1/
2 (10)(2)
2S = 20 meter
c) ketinggian benda saat t = 2 sekon
ketinggian benda saat t = 2 sekon adalah tinggi mula-mula dikurangi jarak yang telah ditempuh benda.
S = 100 − 20 = 80 meter
d) kecepatan benda saat tiba di tanah
V
t2 = V
o2 + 2aS
V
t2 = (0) + 2 aS
V
t = √(2aS) = √[(2)(10)(100)] = 20√5 m/s
e) waktu yang diperlukan benda hingga tiba di tanah
V
t = V
0 + at
20√5 = (0) + (10) t
t = 2√5 sekon
 Kecepatan sudut adalah besarnya sudut yang ditempuh per satuan waktu ( satuan : rad/s). Kecepatan sudut biasa juga disebut kecepatan anguler (anguler artinya sudut)
Kecepatan sudut adalah besarnya sudut yang ditempuh per satuan waktu ( satuan : rad/s). Kecepatan sudut biasa juga disebut kecepatan anguler (anguler artinya sudut)
 Kecepatan sudut adalah besarnya sudut yang ditempuh per satuan waktu ( satuan : rad/s). Kecepatan sudut biasa juga disebut kecepatan anguler (anguler artinya sudut)
Kecepatan sudut adalah besarnya sudut yang ditempuh per satuan waktu ( satuan : rad/s). Kecepatan sudut biasa juga disebut kecepatan anguler (anguler artinya sudut)

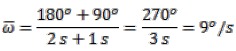 Besar kecepatan sudut rata-rata = 9o/sekon = …. putaran/sekon = ….. radian/sekon ?
Besar kecepatan sudut rata-rata = 9o/sekon = …. putaran/sekon = ….. radian/sekon ?